Digital Signal Processing Overview
R. Port, February 21, 2007
I. Digital Representation of a Waveform
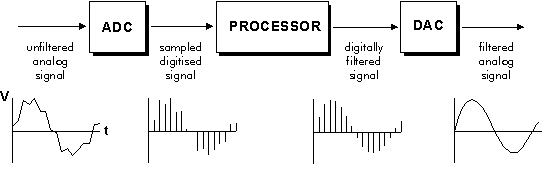
A digital signal processing system takes a continuous sound wave as
input, feeds it through an analog low-pass filter (an anti-aliassing
filter) to remove all frequencies above half the sampling rate (see
Nyquist's sampling theorem). This Analog-to-Digital Converter
(ADC) filters and samples the wave amplitude at equally-spaced time
intervals and generates a simple list of ordered sample values in
successive memory locations in the computer. The sample values,
representing amplitudes, are encoded using some number of bits that
determines how accurately the samples are measured. The Processor
is a computer that applies numerical operations to the sampled waves.
In the figure below, it seems the processor has low-pass filtered the
signal, thus removing the jumpy irregularities in the input wave. When
the signal is converted back into an audio signal by the Digital-Analog
Converter (DAC), there will be jagged irregularities (shown below on
this page) that are quanization errors. Of course, these will lie above
the Nyquist frequency, so the new analog signal (back in realtime)
needs another analog, low-pass filter on output since everything above
the Nyquist frequency is a noisy artefact.
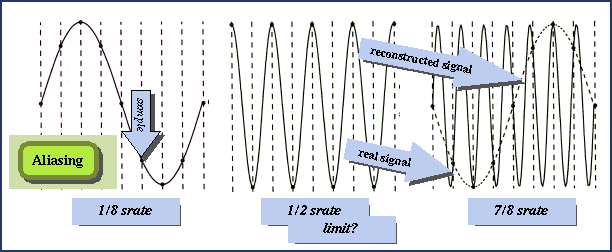
A. Sampling theorem: `Nyquist freq' = (sampling rate)/2
- Aliassing problem (frequencies above
Nyquist
frequency
get mapped to lower frequencies). The leftmost wave below has 8 samples
per cycle (that is, the frequency is 1/8 the sample rate (srate). The
middle curve is the highest frequency that can be represented by
this sample rate. The rightmost figure is much too fast, so the sampled
wave will sound like (be
aliassed as) the slow dotted curve (which is identical to the leftmost
curve).
- Solution: apply input filter before sampling to remove
all unwanted inputs. Any energy
remaining
above the Nyquist frequency will be mapped onto lower
frequencies. Of course, on modern digital equipment, this
filtering is taken care of for you.
- for CD standard, sampling rate = 44.1 kHz, so the Nyquist freq =
22.05 kHz. Of
B. Quantization of amplitude (limited set of amplitude
values). When the sampled signal is converted back into
realtime, of course, there are only assigned values specified at the
sample points. The output signal will just be flat until the next
sample comes along. These flat spots will be perceived by a listener as
a high-frequency signal (above the Nyquist freq), but it will be
noise . So the red curve below must be smoothed (lowpass
filtered) into the green curve below in order to sound right. Of
course, if the sample rate is that of the commercial CD standard, then
this noise will be above the limits of human hearing -- so your own ear
can serve as the lowpass quantization filter. Indeed, since
loudspeakers do not normally produce sounds above 20 kHzm, they too can
also serve as this lowpass output filter.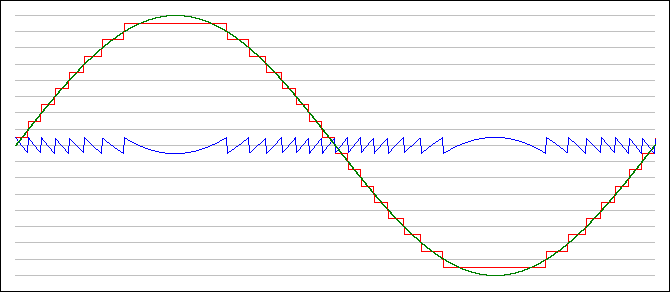
II. Digital Filtering - numerical methods
for
filtering sampled signals. Sample values at each point in time
are
identified with the integers, n. The sampled amplitudes
are
identified here as Xn and ans
will
be the coefficients for modifying each amplitude.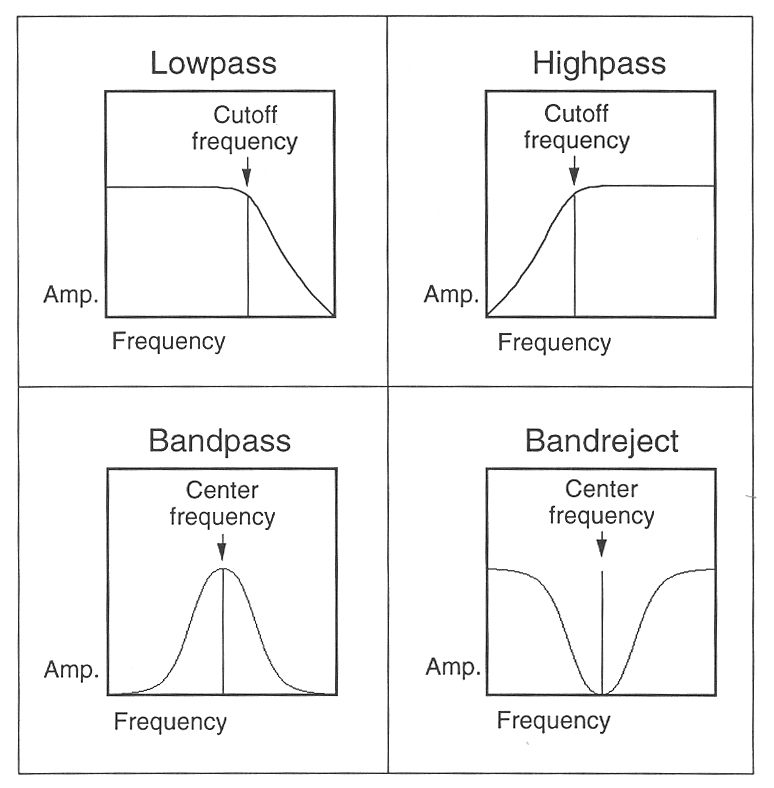
A. Primitive low-pass digital filter -
For
example,
a running average of 2 (or more) adjacent samples. Thus, take
sample
Xn
and sample Xn+1, add their amplitudes, and divide
by 2. This is equivalent to taking half the amplitude of sample Xn
and adding half of Xn+1. (The mathematical term for
such
a `running average-like' calculation is convolution: apply the
operation,
move over one time step, apply it again. Repeat until you run out of
samples.)
The number of coefficients used is the order of the filter, so
the
`running average of 2 adjacent samples' has order 2.
Y0
= a-2X-2
+ a-1X-1 +
a0X0
+...amXm,
where
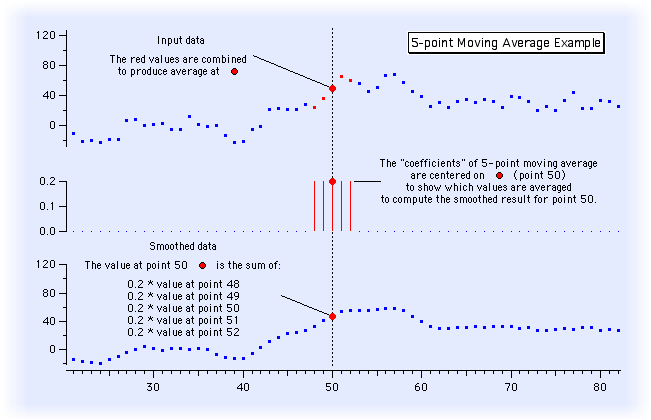
- Here is a digital signal processed by a 5th-order moving-average
filter. It averages 5 adjacent samples by multiplying each by .2, then
summing. You can see how the signal is smoothed in the bottom display.
The higher-frequency components of the function have been
removed. The equation for this filter is: Y 0 =
.2X -2 + .2X -1 + .2X 0 + .2X +1
+ .2X +2 It is illustrate below as the 5 red
lines in the middle panel.
- Impulse response: response of the filter to a single
sample
of
1 embedded among adjacent samples of 0 -- roughly equivalent
to tapping a bell or pinging the resonator. Below the red impulse
of 1 causes the filter to respond with a fading oscillation.

B. Primitive high-pass filter
- `first-difference filter' - Subtract adjacent samples to
flatten
out a lower-frequency trend in the sampled data. Rapid changes
between adjacent samples are preserved, but the value that both samples
share is dropped away. So an input sequence like
[2,6,3,7,4,8,5,9] comes out of the filter as [+4,-3,+4,-3,+4,-3,+4].
Y0 =
a0X0
- a1X1
- for various filters, the coefficients may be positive or
negative.
Notice that it matters very little if we use X-1 and X0
or X+1 and X0 -- it just shifts the
data points
one sample point to the left or right.
C. General properties
- A digital filter can be made to exhibit any spectral shape you want.
And mathematical methods for finding the correct form of the equation
exist.
- Generally, to make a filter with more peaks (or `poles' as
they are
sometimes
called) or for sharper cutoffs and smaller ripples, more coefficients
are
required.
III. Fast Fourier Transform, a method
for doing
general Fourier analysis on sampled signals efficiently. One
specifies
the number of sample points employed (which implies the time window for
the spectrum) as a power of 2. Sampling, eg, at 16k Hz means 1 ms = 80
samples, so a 256 point FFT looks at 3.2 ms and a 512 point FFT looks
at
6.4 ms. At the CD standard, 512 sample points is about 1 ms.
IV. Linear Predictive Coding (LPC). A
method of speech coding that constructs a digital filter that will
model a short segment
(called
a frame) of a speech waveform using many fewer bits than the
explilcit waveform itself requires. The coefficients and other
parameters are then used to resynthesize the original speech.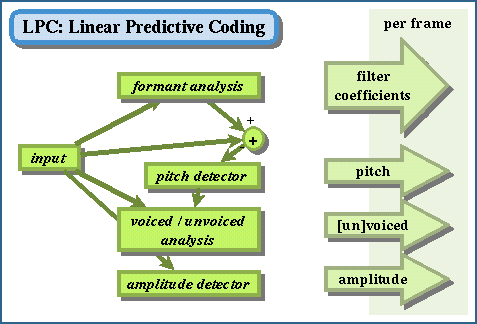
- LPC first determines the portions of the speech frame (often
about 20 ms long) that are voiced from the voiceless. For the voiced
portions, it identifies the F0 (pitch). It also measures the amplitude
of the frame.
- The LPC algorithm computes a set of filter coefficients
(where the LPC order
is
the number of computed coefficients - usually between 6 and 20) that
will reconstruct a model of the
input signal.
- This set of coefficients can then be used to approximately
reconstruct
(ie, synthesize)
many sample points from a small number of coefficients plus indication
of whether to excite the filter with noise or pitch pulses, and the
location
of pitch pulses in time (eg, the F0). Thus, a frame containing 2 pitch
periods (about 20
ms),
during which the vocal tract shape does not change very much, would
contain
(if sampled at 10kHz) 200 samples. A set of only 12-16 LPC coefficients
plus
2 impulses (one for each pitch period) can generate the whole frame of
200 samples well enough to yield quite natural sounding speech.
- Rule of Thumb 1 is: 2 coefficients are needed
for each
spectral
peak that one wishes to model, including a `peak' at frequency 0 to
model the overall downward slope of the spectrum. Thus 12 coefficients
will model about 5 formants in the frame plus the spectral slope.
- Rule of Thumb 2 is: as the frames get longer (to
economize on
bits)
the sensitivity (of the LPC representation) to change
in
the signal gets weaker. But as the frames get shorter, you will
use more coefficients per second, so the
economy
of encoding is reduced.
- Notice that the LPC algorithm calculates the spectrum without
differentiating
the source spectrum from the filter spectrum, the
LPC
coefficients model the product of both. This is because LPC
uses
only a unit pulse (a single sample with the value of 1) to
simulate a glottal pulse (which looks quite
different than a pulse).
- Some uses of LPC in the phonetics lab include (1) since the pitch
pulses are extracted from the signal
before the LPC encoding, it is
a useful lab tool for manipulating F0 artificially. You
just replace the file of pulses with a different file. (2) The LPC
spectrum offers a description of the speech spectrum that is easier to
interpret than the FFT. Indeed, programs that extract the formants of speech
usually do LPC first and compute the LPC spectrum, then seek the peaks
that are formants. (Wavesurfer does it this way.)